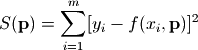1、概念简介
假设有一组数据(x[i], y[i]),我们知道它们之间的函数关系y=f(x),通过这些已知信息,我们需要确定函数中的一些参数项。
例如,如果f是一个线性函数:f(x) = k*x + b,那么参数k和b就是我们需要确认的值。
如果这些参数用P表示的话,我们会得到一组P值使得如下公式中函数S的值最小:
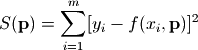
这种算法称之为:最小二乘拟合(Least-square fitting)。
公式中的m表示的是样本的记录条数,通过逐条的计算得到的和进行比较,得到S(P)的最小值。
当然这个计算如果用人来做的话,样本数多的情况下几乎无法完成,所以,一般我们用scipy库来做。
2、实际用途
假设我们掌握了若干条某城市的房价(y)与面积(x)的对应数据,且通过绘制散点图发现其相关性大致如图所示:
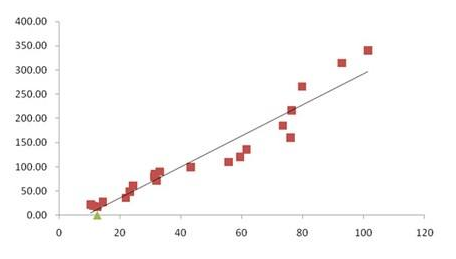
我们大致猜测,房价y与面积x之间是线性相关的关系,那么一定存在某个公式:y = k*x + b,能够最好的拟合现有数据(注:完全与现实数据拟合的情况是不存在的,除非所有的散点都恰好在同一个直线上)。
为了能够获得根据面积自动预测房价的超能力,我们需要知道参数k和b的具体值。
因为当我们掌握了这组拟合度最好的值,我们才能预测出最接近实际的房价。
所以,我们通过最小二乘拟合的方式,来获得最接近实际情况的k和b的值,从而实现对房价的预测。
ps:当然,实际情况是,房价并不只与面积相关,还与户型、地理位置、周边环境、楼层等多个因素相关,我们为了方便举例,忽略了其他因素。
同样的,在深入学习了机器学习的理论之后,我们还可以将其应用到更加广的范围内,例如:价格、人口、环境等,但那些情况都有一个共同点:一般他们不会是一个简单的线性函数,实际情况更加复杂。
3、使用方法(python演示)
所需资料:
- 一组包含20条房产价格和面积对应关系的数据
- PYTHON运行环境
实现步骤(后面会给出完整代码打包下载)
1)数据整理:将已掌握的数据整理存储为csv逗号间隔文件,方便读取。
我们将使用这样一组数据作为参考数据,用来模拟房价的计算。
真实情况下,我们可以使用已掌握的数据,或通过程序抓取等方式来获得原始数据。
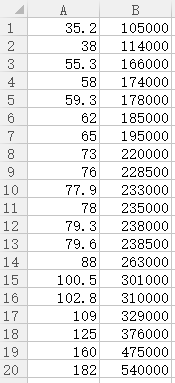
很简单,将excel文件另存为CSV(逗号分隔)即可。
存储后的csv文件,选择打开方式为记事本,我们可以看到:
这时候我们已经完成了简单的数据整理,可以将文件存放到指定目录下,留待程序调用。
2)数据读取:在python中读取csv文件
请参考以下代码:
import scipy as sp
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
data = sp.genfromtxt("D:\\Python\\ML\\test.csv", delimiter=",")
x = data[:, 0]
y = data[:, 1]
通过执行print(x)或print(y),可以看到我们已经成功将面积赋给了x,房价赋给了y,为后面的运算打下了基础。
3)绘制散点图:在pyplot中绘制数据分布散点图
散点图的绘制其实非常简单,交给pyplot来办就可以了:
plt.scatter(x,y)
plt.title("模拟演示数据分布图")
plt.xlabel("面积x")
plt.ylabel("房价y")
plt.autoscale(tight=True)
plt.grid()
plt.show()
绘制出的效果如下:
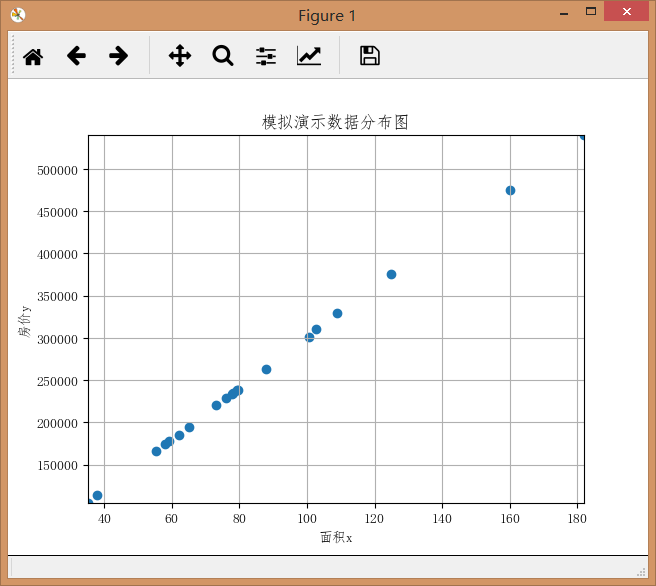
我们可以看到,其分布大致是一条直线(实际上是有微小偏差的),这就给我们一种直观的判断,房价与面积,应该是线性相关的,但究竟如何计算?我们要拿着一个尺子,去测量x轴和y轴的值吗?当然不用。
4)计算f(x)=k*x + b中的最优参数项k和b的值:
参考代码:
def error(f, x, y):
return sp.sum((f(x)-y)**2)
fp1, residuals, rank, sv, rcond = sp.polyfit(x, y, 1, full=True)
print("[k,b]参数值为 %s 时,最接近演示数据结果。" % fp1)
计算结果:

这里我们得到,当k=2968.52680507,b=2296.35884168时,我们的公式计算结果最接近演示数据。
等等,我们似乎错过了什么?
通过观察演示数据,事实上我们不难发现,我是按照大约3000元/㎡的价格来计算的(真的好便宜的房价啊),然后对结果进行了微调,有的增加了几千元,有的减少了几百元,从而使数据不是非常精确的在同一条直线上。但计算的结果,为什么不是k=3000,b=0呢?
事实上,假设我们已知计算公式的情况下,我们得出的结果,也不是完全一致的,而实际上,可能存在多个参数项的组合,是可以计算出相同结果的,所以程序给出的答案,未必是错误的。下一步我们就来验证一下。
5)验证结果:我们将参数代入方程式,看看计算结果是否接近已知结果:
操作代码:
for i in range(20):
print("当x值为%d时,y的预测值为:%.2f,演示数据中为:%d, 误差为:%d" % (x[i], (x[i]*fp1[0]+fp1[1]), y[i], y[i]-(x[i]*fp1[0]+fp1[1])))
结果如下:
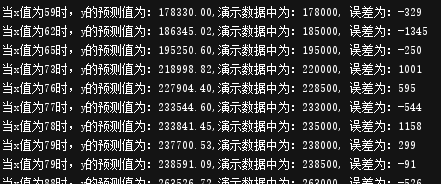
你可能会说,误差也很大啊,最大误差有2000多呢。是的,因为原始数据被调整了。
不过,没关系,我们再来计算以下几组数值,看看通过我们设计数据(y=3000*x)的公式来计算的结果误差有多少:
for i in (80,90,100):
print("当面积为%d平米时,预测值为:%.2f,计算值为:%d,误差为:%d" % (i, (i*fp1[0]+fp1[1]), i*3000, i*3000-(i*fp1[0]+fp1[1])))
我们以80、90、100平米,比较了机器预测结果与实际公式之间的误差:

由此可见,误差已经很微小了,足够进行房价预测了。
4、总结
这样我们就完成了一个非常小的房价预测的软件,如果再增加更多的样本,将会获得更加精准的预测数据。
然后还是要补充的是,通过最小二乘拟合来做的模拟预测,只是为了让我们快速理解机器学习的基本思想理念:让机器自己去尝试不同的参数值组合,找到最接近现实的参数组,从而实现预测。而实际应用中,要远远的比这复杂的多,机器学习博大精深,涉及学科众多,尤其是数学、概率、统计方面,所以要学的还很多,这只是相当于机器学习中的“Hello World!”
附:本文源码和csv文件